ABY3 Research Notes

安全三方计算的机器学习框架

多方联合机器学习是目前研究的热点之一，但其中带来的安全隐患是其中不可避免的研究课题。在2018年CCS上，Payman Mohassel 等人提出了ABY3的三方联合机器学习架构，由地位均等的三个服务器执行安全三方计算协议，共同训练和估计模型。值得注意的是文章用到机器模型限于监督学习下的线性回归、逻辑回归和神经网络。ABY3架构能够有效地在算术、二进制和garbled电路的三方计算中进行转换；并提出了高效地定点数(fixed-point)乘法方案，用以优化计算分段多项式函数。

机器学习模型训练和中间参数计算都是用十进制，不能处理模块化算数，一般有两种处理方法，一是将十进制数(浮点数)转换为整数，用最低有效位表示小数部分，选择一个足够大的模数，使得商(wrap round)足够小。但是在类似随机梯度下降的表尊训练算法中需要执行数百万计的运算，这种方法会使得浮点数乘法带来很大的误差。模数大又意味着对乘法的消耗大，这使得计算效率大大降低。另外一种是使用安全多方计算中的布尔乘法电路计算定点数乘法。布尔电路可以用秘密共享或garbled电路估计，这会使得协议的交互次数和通信量增加。

大多数机器学习都进行算术运算、非算术运算和分段多项式函数之间转换，比如，按顺序包括加法乘法、近似激活函数和ReLU函数。每一种运算都有其高效的运算方式。算术运算和非算术运算可以利用秘密共享进行计算，而分段多项式函数可以用二进制秘密共享或姚电路实现。在不同的秘密共享方案之间的转换的成本很高，这是研究机器学习隐私保护的研究难点之一。

秘密共享

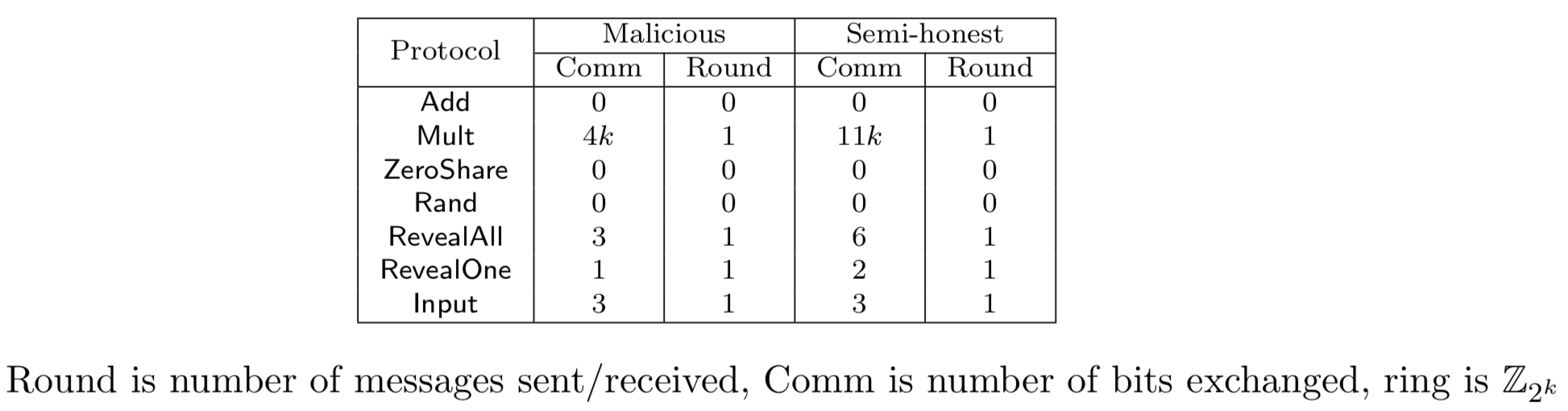
在一个半诚实模型中，一个秘密 $x \in \mathbb{Z}_{2^k}$ 随机抽样成 $x_1, x_2, x_3 \in \mathbb{Z}_{2^k}$，并且有 $x = x_1+x_2+x_3$，秘密分块分布成三个部分 $\{(x_1, x_2),(x_2, x_3),(x_1, x_3)\}$，每个拥有者$i$都持有第 $i$部分。因此秘密共享可以表示成 $[\![ x ]\!]^{\mathsf{A}}$作为一个三元组 $(x_1, x_2, x_3)$，每一方都拥有一对秘密共享。可以观察到三方中的任意两方能够恢复出秘密$x$，意味着这个方案最多只能容忍一方是恶意的。在算数、二进制和姚电路秘密共享中每个算子的消耗是如下：

第$i$方把他的秘密对$x_i$发送给第$i+1$方，通过三个秘密分块相加，每一方都能够在本地重构恢复出$x$。同样的，第$i-1$方发送$x_{i-1}$给$x_i$，他也可以在本地重构出秘密。三方的秘密共享在$\mathbb{Z}_{2^k}$的算术操作如下

• 加法：$[\! [x] \!]+[\![ y ]\!] = [\![ x+y ]\!]:=(x_1+y_1,x_2+y_2,x_3+y_3)$
• 和常数$c$的加减法：$[\![ x ]\!] \pm c=[\![x \pm c]\!]=(x_1 \pm c, x_2, x_3)$
• 和常数$c$的乘法：$[\![ cx ]\!] = (cx_1,cx_2, cx_3)$
• 两个秘密共享的乘法$[\![ x ]\!]$和$[\![ y ]\!]$，这个过程必须产生交互 $\begin{align*} [\![ xy ]\!] & = (x_1+x_2+x_3)(y_1+y_2+y_3) \\ & = x_1y_1+x_1y_2+x_1y_3 \\ & + x_2y_1+x_2y_2+x_2y_3 \\ & + x_3y_1+x_3y_2+x_3y_3 \end{align*}$

每个参与方都能计算交叉项，定义$[\![ z ]\!]=[\![xy ]\!]$，使得每一方$i$都有$z_i$
$\begin{align*} z_1 &:= x_1y_1+x_1y_2+x_2y_1 \quad + \alpha_1 \\ z_2 &:= x_2y_2+x_2y_3+x_3y_2 \quad + \alpha_2 \\ z_3 &:= x_3y_3+x_3y_1+x_1y_3 \quad + \alpha_3 \end{align*}$

每一方$i$可以本地计算出$z_i$获得$[\![ x ]\!]$和$[\![ y ]\!]$的共享分块，要求所有各方都持有三个秘密分块当中的两个秘密分块。协议让第$i$方把$z_i$发给第$i-1$方。额外的部分$\alpha_1,\alpha_2,\alpha_3 \in \mathbb{Z}_{2^k}$随机化$z$的秘密共享。这里随机元素有$\alpha_1+\alpha_2+\alpha_3=0$，第$i$方只知道相应部分的随机数，并获得随机密钥$k_i$和$k_{i+1}$的一个伪随机函数(PRF)F。这个随机数不需要三方之间的相互互动。这里，第$i$方通过计算$\alpha_i = F_{k_i}(j)-F_{k_{i+1}}(j)$得到第$j$个秘密共享。同一个伪随机函数PRF的密钥是通过共享在$\mathbb{Z}_{2^k}$上的随机值得到。特殊的，为了分享第$j$次的一个随机数，第$i$方令$r_i=F_{k_i}(j), r_{i+1} = F_{k_{i+1}}(j)$。 $(r_1,r_2,r_3)$ 的随机值构成了$r=r_1+r_2+r_3$重秘密共享。

上述秘密共享是一个半诚实模型的(3,2)门限协议，只需要三方中的任意两方均可重构出秘密。显然这个协议不能抵抗敌手的攻击，敌手在乘法或者输入秘密共享中发送一个错误值，其他各方都得不到正确的输出。

定点数计算

点数计算文中给了Secureml的方案不work的原因，两方计算的定点数计算不能推广到三方中。在计算过程中会产生两种误差。一是二进制进位误差，两方秘密共享一个定点数，先把它映射到环$\mathbb{Z}_{2^k}$上，使得$[\![ x ]\!]:=(x+r, -r)$，其中$r$是$\mathbb{Z}_{2^k}$上的随机数。在环$\mathbb{Z}_{2^k}$上加减法容易操作，但乘法不易操作，因其要在环上除以$2^d$。在三方中要计算定点数$x =yz$，则需要计算环$\mathbb{Z}_{2^k}$上的$[\![x^\prime ]\!]=[\![y ]\!][\![z ]\!]$，其中$[\![x^\prime ]\!]:=[\![x^\prime/ {2^d} ]\!]$。理想情况下，$[\![ x^\prime ]\!]:=(x^\prime+r^\prime, -r^\prime)$的两个秘密共享可以在本地被$2^d$整除，从而获得两个$k$比特长的共享$[\![\tilde{x} ]\!]:= (\frac{x^\prime_1}{2^d}, \frac{x^\prime_2}{2^d})$，并拥有$x = x^\prime / x^d = \tilde{x}$。但是在世纪操作中，等式并不成立，因为$x$除以$2^d$之后，从前$d$比特位开始去掉第$d+1$比特位的进位。换句话说，在加法$ x^\prime_1 + x^\prime_2 = (x^\prime + r^\prime) + (-r^\prime) \bmod 2^k $的第$d$位会产生一个进位(carry)，但是每一分享都分别除以$2^d$，可以消除这个进位。这个误差的概率大小为$2^{-d}$，鉴于定点运算的精度的要求，这一点误差可以接受。事实上，Secureml文中证明，当$d$的取值足够大的时候，浮点数计算的误差对训练模型的精度没有影响。二是因为共享环模数$2^k$二进制补码带来的误差，计算机在处理负数时一般采用2的补码的方法。在计算$x^\prime / 2^d$二进制补码的时候，即设置$x^\prime$的比特位向下(左上右下)移动$d$个比特位，填满$x^\prime$的最高有效位(MSB)的前$d$个位置。但是$x^\prime$在$\mathbb{Z}_{2^k}$中的秘密共享中，填满$d$个MSB位会失败。比如$x^\prime = -2^{k-1}$，在二进制的2的补数是$100…000$，而$x^\prime / 2^d$ 表示成$1…100…000$，这里前面有$d+1$个$1$。但是秘密共享$x^\prime_1, x^\prime_2$的MSB都有0，这样导致的结果是秘密共享除以$2^d$后，这两个秘密共享高位最少有$d+1$个0。这样的秘密共享重构出错误的结果。比如，当结果的高位有$d$或$d-1$个0的时候会出现一个MSB相反，会产生一个大的误差。相反，若$x^\prime_1, x^\prime_2$的MSB都是1，并且溢出丢弃掉，当它们在除以$2^{-d}$后，进位变成了$1+1+1$，这使得$d$个MSB错误的变成1，这与条件$x^\prime$的MSB是1相矛盾。
为了解决上述问题，最普遍的方法(源自Secureml)是找到两个大整数让$x^\prime$的计算不会轻易的溢出。假设$\lvert x^\prime \rvert < 2^l \ll 2^k$，这里$x^\prime$即为2的补码。这就保证了$x^\prime_1$的MSB和$x^\prime_2$的MSB只有极小可忽略的概率相等。为什么是会这样呢？假设$x^\prime_1 := x^\prime + r^\prime, x^\prime_2=-r^\prime$，假设$r^\prime \ne 0$，$r^\prime$和$-r^\prime$的MSB始终是相反的。当$x^\prime$是正数时，$x^\prime_1$和$x^\prime_2$的MSB相同的概率，就是$r^\prime$的前$k-l$比特全是1并且在$x^\prime + r^\prime$的第$l$比特产生一个进位的概率。由于$r^\prime$是随机均匀的，$r^\prime$的高位(前面)存在许多$1$的概率是$2^{l-k}$，若选择适当的$l,k$，这个概率可以忽略不计。同样也可以论证$x^\prime$是负数的情况。
因此，上述两个误差导致定点数计算时不可避免。当秘密共享被各自截断是，会出现进位丢失的情况，产生$2^{-d}$的误差，这种误差在绝大多数的秘密共享方案都存在，所得到的数值“足够接近”真实值。通过调节$d$的大小可以控制误差的大小。另一个误差来源于秘密分块的符号，计算符号的不正确也会导致结果错误。正因为如此，导致两方方案不能扩展到三方协议中。若$[ \![ x ]\!] = (x+r_1+r+2, (-r_1), (-r_2))$，显然需要截断两个进位，出现的误差变成$2^{-d+1}$，这个误差增大了一个量级。另外，$\lvert x \rvert \leq 2^l$ 的范围确保不了大的误差以小概率事件发生。两个截断进位的操作，让误差的必要条件更复杂。由于$r_1, r_2$是随机均匀和相互独立的，约束条件$\lvert x \rvert \leq 2^l$使得$x_1,x_2,x_2$的符号不能正确扩展。