Reading Falcon Note 1

诚实方占多数的恶意安全模型下Secure Deep Learning框架

1. 基本思想

Falcon设计了一个三方安全计算的机器学习框架。三方主要包括数据拥有者(data holder, DH)，需要机器学习服务的查询用户(query users, Users)和提供机器学习服务的计算服务器(computing servers, Server). Falcon框架包括两个阶段：训练阶段和推导阶段。训练阶段由DH提供数据，Server计算出机器学习模型；推导阶段User向Server发出查询请求，Server提供一个训练模型。DH把数据用重秘密共享(Replicated secret sharing)方式把数据分布到不同3个服务器上。三个服务器利用这些共享数据训练出各自不同神经网络模块，用户此时可以提交查询，并得到模型的秘密分块。用户通过重构这些秘密分块重构出完整的训练模型。这种方式的优点是，因为服务器只有秘密分块，因此DH的数据对三个服务器都是完全隐私的，Users的查询请求也对服务器也是保密的。Falcon使用安全多方计算设计协议。安全性满足恶意安全，如果一方是恶意腐败的(corruption)，协议能够保证有正确的输出或者终止协议的恶意行为，不会输出错误的结果。同时文章也是开源的。同时文章也对不同的机器学习安全多方计算协议进行比较，如下图。

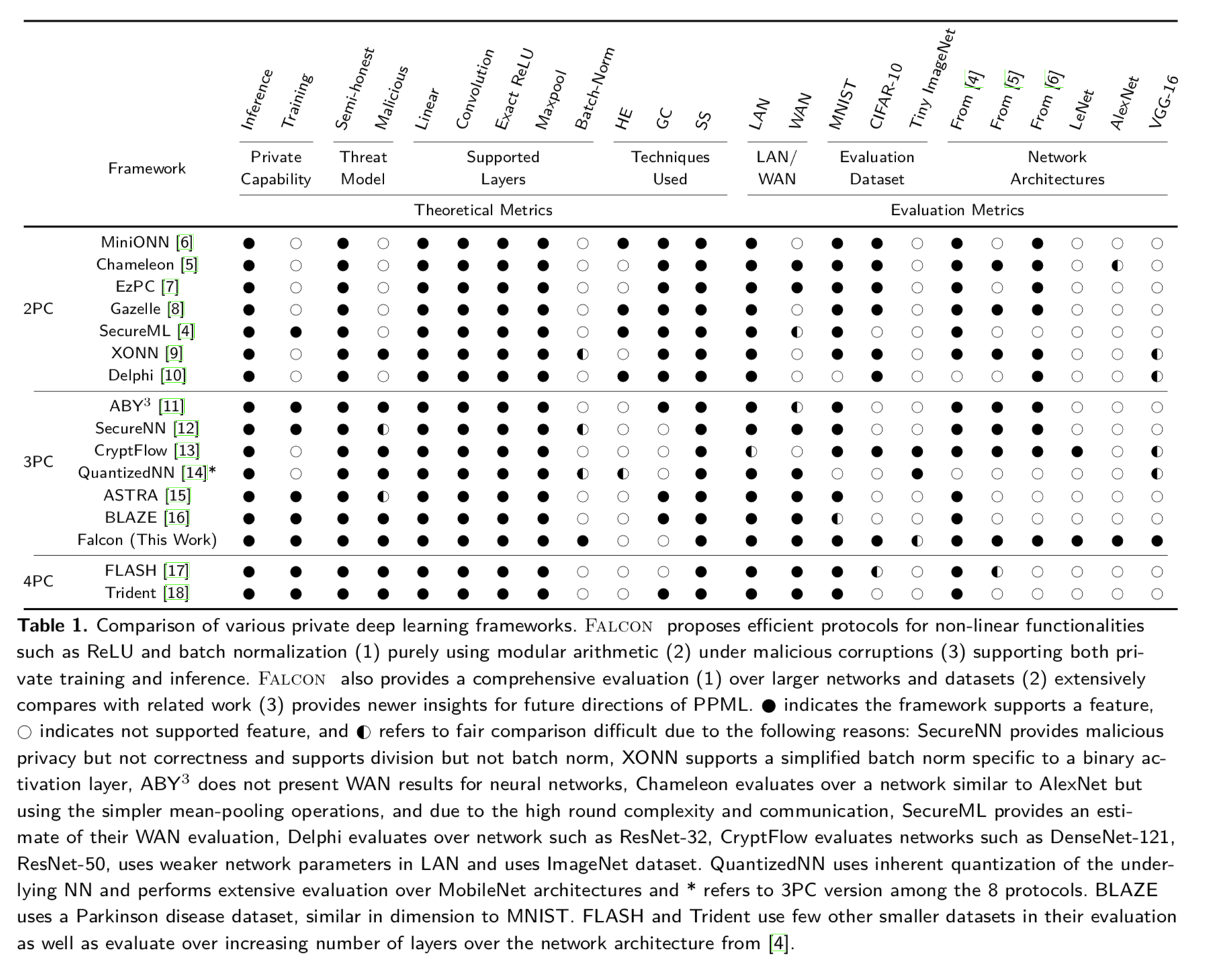
2. 算子

ABY3依赖于高效进GC计算非线性函数，不同于简单的模数计算。

相关随机性 文章利用用$\text{PRF}$(伪随机函数)设计两个基本的随机数生成器。$(3,3)$随机性，即各方随机生成$\alpha_i$，使得$\alpha_1 + \alpha_2 + \alpha_3 = 0$。$(2,3)$随机性，即各方随机生成$(\alpha_i, \alpha_{i+1})$，使得$\alpha_1 + \alpha_2 + \alpha_3 = 0$。给定一个$P_i$和$P_{i+1}$之间的随机密钥$k_i$，令$\mathsf{cnt}$ 是每次调用后递增的计数器。

初始化 $P_i$选择一个随机种子$k_i$，并把它发送给$P_{i+1}$。 一般随机性：令$F$是一个PRNG(伪随机数生成器)

• $ \alpha_i = F_{k_i}(\mathsf{cnt}) - F_{k_{i-1}}(\mathsf{cnt}),\; \mathsf{cnt}++ $
• $ (\alpha_i, \alpha_{i-1}) = (F_{k_i}(\mathsf{cnt}), F_{k_{i-1}}(\mathsf{cnt})),\; \mathsf{cnt}++ $

截断数对：$[\![ r]\!], [\![ r^\prime]\!] = [\![ r / 2^d]\!]$

关联隐私比较随机性：

• 随机取样比特$[\![ b]\!]^2$
• 利用位插入$[\![ b]\!]^2 \rightarrow [\![ b]\!]^p$
• 随机取值$m_1, \cdots, m_k \in \mathbb{Z}_p$
• 计算并公开$m^{p-1}_1, \cdots, m^{p-1}_k$
• 移除为0，留下为1的值，设置一个大的$k$值，均摊开销提高效率，共计$\lceil \log_2 p \rceil$轮。

关联封装函数随机性：

• 随机取样比特$[\![ r_i ]\!]^2, \; i \in [l]$
• 执行位分解得到$[\![ r_i ]\!]^L$
• 执行位插入$[\![ r_i ]\!]^2 \rightarrow [\![ r_i ]\!]^p$
• 利用全加器计算最终进位

关联ReLU随机性：

• 随机取样比特$[\![ b]\!]^2$
• 利用位插入$[\![ b]\!]^2 \rightarrow [\![ b]\!]^L$

线性操作 令$a,b,c$是公共参数，$[\![ x ]\!]^m$ 和 $[\![ y ]\!]^m$是秘密共享，各方在本地计算

• $[\![ ax + by + c ]\!]^m := (ax_1 + by_1 + c, ax_2 + by_2, ax_3 + by_3)$。

乘法 要使两个秘密共享相乘$[\![ x ]\!]^m = (x_1, x_2, x_3)$ 和 $[\![ y ]\!]^m = (y_1, y_2, y_3)$

• 各方本地计算$z_1 = x_1y_1+x_2y_1+x_1y_2, z_2 = x_2y_2+x_3y_2+x_2y_3, z_3 = x_3y_3+x_1y_3+x_3y_1$
• 由$z_1, z_2, z_3$形成$(3,3)$门限共享$[\![ z=x \cdot y ]\!]^m$
• 各方执行重共享协议，利用$(3,3)$随机性生成$(2,3)$门限共享，即第$i$方发送$\alpha_i + z_i$ 给第$i-1$方，${\alpha_i }$形成$(3,3)$零共享。

重构$[\![ x ]\!]^m$

• 半诚实模型中，每方发送一个环元素给下一方，即$P_i$ 发送共享$x_i$ 给$P_{i+1}$
• 恶意模型中，第$i$方发送共享$x_i$给$P_{i+1}$，再发送共享$x_{i+1}$给$P_{i-1}$，若两个值不同，则中止协议。此轮协议是单轮通信。

秘密共享 输入两个随机共享$[\![ x ]\!]^L$ 和 $[\![ y ]\!]^L$，一个随机比特$[\![ b ]\!]^2$，通过判断$ b = 0 \; \text{or} \; 1 $输出$[\![ Z ]\!]^L = [\![ x ]\!]^L \; \text{or} \; [\![ y ]\!]^L$。

• 获取共享随机比特$[\![ c ]\!]^2$，预计算$[\![ c ]\!]^L$
• 公布比特$(b \oplus c) = e$，若$e = 1$，设置$[\![ d ]\!]^L = [\![ 1 - c ]\!]^L$；若$e = 0$，设置$[\![ d ]\!]^L = [\![ c ]\!]^L$
• 计算$[\![ z ]\!]^L = [\![ (y-x) \cdot d ]\!]^L + [\![ x ]\!]^L$，其中用乘法协议计算$[\![ (y-x) \cdot d ]\!]^L$

与公开位$b$异或 给定共享比特$[\![ x ]\!]^m$和一个公开位$b$

• 各方在本地计算共享比特$[\![ y ]\!]^m = [\![ x \oplus b ]\!]^m$，注意到$ y = x+b-2b \cdot x $
• b是公开的，这属于线性运算，在半诚实和恶意的对手模型中都能计算。

从$[\![ x ]\!]^m$到$[\![ \beta ]\!]^m$估计$[\![ (-1)^\beta \cdot x ]\!]^m$ 令$\beta \in \{0,1 \}$，执行乘法协议获得$[\![ (1-2\beta)\cdot x ]\!]^m = [\![ (-1)^\beta \cdot x ]\!]^m$

3. 隐私比较

各方持有$\mathbb{Z}_p$中的共享比特$x$和公开值$r$，计算$ x \ge r$。协议如下图 在协议中需要用随机比特$\beta$盲化，若没有这一步，$\beta ^ \prime$将会泄露输出$ (x \leq r) $的信息。每一位的比特都是相对独立，单个盲化比特位$\beta$隐藏$(x \ge r) \; \text{or} \; (r > x)$的计算。该协议将简单模块算法与恶意安全模型相结合。 根据协议看到：

• 步骤2表示通过估计$2\beta-1$共享计算$u[i]$，再计算$ (2\beta - 1)(x[i] - r[i]) $，调用乘法协议在一轮交互通信完成
• 步骤3、4是本地简单的计算，比如$[\![ w[i] ]\!] = (w[i]_1, w[i]_2, w[i]_3)$能用$w[i]_j = x[i]_j + \delta_{j1}[i] - 2r[i]x[i]_j$计算，这里$ j \in {1, 2, 3}$, $\delta_{ij}$ 是克罗内克函数(Kronecker delta function)，即$i=j, \; \delta_{ij}=1$，否则$\delta_{ij}=0$
• 步骤6用连续调用较小字符串的乘法协议，在$\log_2l+1$计算随机盲化因子，故多出1轮通信
• 步骤7、8在本地计算

4.Warp函数ReLU和DReLU

文章定义Warp函数来计算比较。wrap 函数定义 $\mathsf{wrap}_2$ 和 $\mathsf{wrap}_3$ 为各方秘密份额的函数，并在将共享看作整数并相加，有效地计算“进位比特”。

$\mathsf{warp}_{3e}(a_1, a_2, a_3, L)= \begin{cases} 0 & \text{if} \; \sum^3_{i=1}a_i < L \\ 1 & \text{if} \; L \leq \sum^3_{i=1}a_i < 2L \\ 2 & \text{if} \; 2L \leq \sum^3_{i=1}a_i < 3L \end{cases}$ $\mathsf{warp}_{3}(a_1, a_2, a_3, L)= \mathsf{warp}_{3e}(a_1, a_2, a_3, L) \pmod 2$

$\mathsf{wrap}_3$函数中共享$ a_1, a_2, a_3 $与底层秘密 $a$ 的最高有效位 (MSB) 之间关系密切。$ a=a_1+a_2+a_3 \pmod{L} $作为$a_i$在模$L$的共享，用逻辑电路(如行波进位加法器)计算此和，可以计算$ \text{MSB}(a) = \text{MSB}(a_1) + \text{MSB}(a_2) + \text{MSB}(a_3) +c \pmod{2} $，$c$是来自上一索引的进位比特。上一索引的进位比特$c$只在$a_i$的模$L/2$上计算的$\mathsf{wrap}_{3e}$函数。这最后一个操作和计算$2a_i$模$L$上的$\mathsf{wrap}_{3e}$函数意义相同。算法2给出了$\mathsf{wrap}_3$函数的计算。 算法中参数的计算：

其中$\delta_e, \alpha_e$是wrap函数，等式(1)中，$r, a, x \in [0, L-1] $和$ r \equiv a+x \pmod{L} $。因此，若$ a+x \ge L $，当且仅当$ r < x (\text{or} \; x \ge r+1) $，假设$ \theta_e $是$a_1, a_2, a_3$的wrap函数即： $a = a_1 + a_2 + a_3 - \theta_e \cdot L$ 在定点算术计算中，正数是前$2^{l-1}$位，最高有效位MSB为0；负数是后$2^{l-1}$位，最高有效位MSB为1。定义ReLU的导数函数为：

它与定点数表示$\text{DReLU}(a) = 1-\text{MSB}(a)$的最高有效位有简单的联系。通过联系$\mathsf{wrap}_3$函数，写成如下等式： $\mathsf{DReLU}(a) = \mathsf{MSB}(a_1) \oplus \mathsf{MSB}(a_2) \oplus \mathsf{MSB}(a_3) \\ \oplus \mathsf{wrap}_3(2a_1, 2a_2, 2a_3, L) \oplus 1 \tag{6}$ 从DReLU函数计算ReLU函数，可以用简单的秘密共享完成，通过对$a$的共享和$\text{DReLU}(a)$的共享执行乘法协议。$P_1, P_2, P_3$持有$\mathbb{Z}_L$上的共享$a$，均得到$ \mathsf{ReLU}(a) $的共享

• 各方利用算法2获得$\mathsf{wrap}_3(2a_1, 2a_2, 2a_3, L)$
• 通过等式6计算共享$[\![ b]\!]^2, b=\mathsf{DReLU}(a)$
• 在$ {a, 0} $上，用$b$的选择执行秘密共享协议得到输出