About BLAZE Reading Note

BLAZE，三方安全计算的机器学习方案。

回顾以往看到的机器学习隐私保护的方案中，安全多方计算在ML中的用到的十分广泛，也很重要。因为可以根据参与方的不同数量可以设计不同的机器学习隐私保护协议。回顾以往的论文，两方参与计算的机器学习方案有SecureML、Gazelle和Delphi等，三方参与计算的方案有ABY3、BLAZE和Falcon等。也有一些方案存在四方同时参与，比如FLASH。通常这些方案都解决回归（线性和逻辑）、卷积、比较和求最大的操作。安全两方计算通常只能满足半诚实模型下，如果两方中一方是恶意的，方案的效率会很低，比如XONN。三方及以上的方案可以满足存在一方是腐败方，其它是诚实方的恶意安全模型。BLAZE是Arpita Patra等人在2020NDSS上发表的论文，旨在解决外包计算中的ML算法问题。文章主要完成了:

• 设计一种点基协议，使在现阶段的通信与向量无关
• 用新的截断方式避免高的RCA开销并固定通信轮数

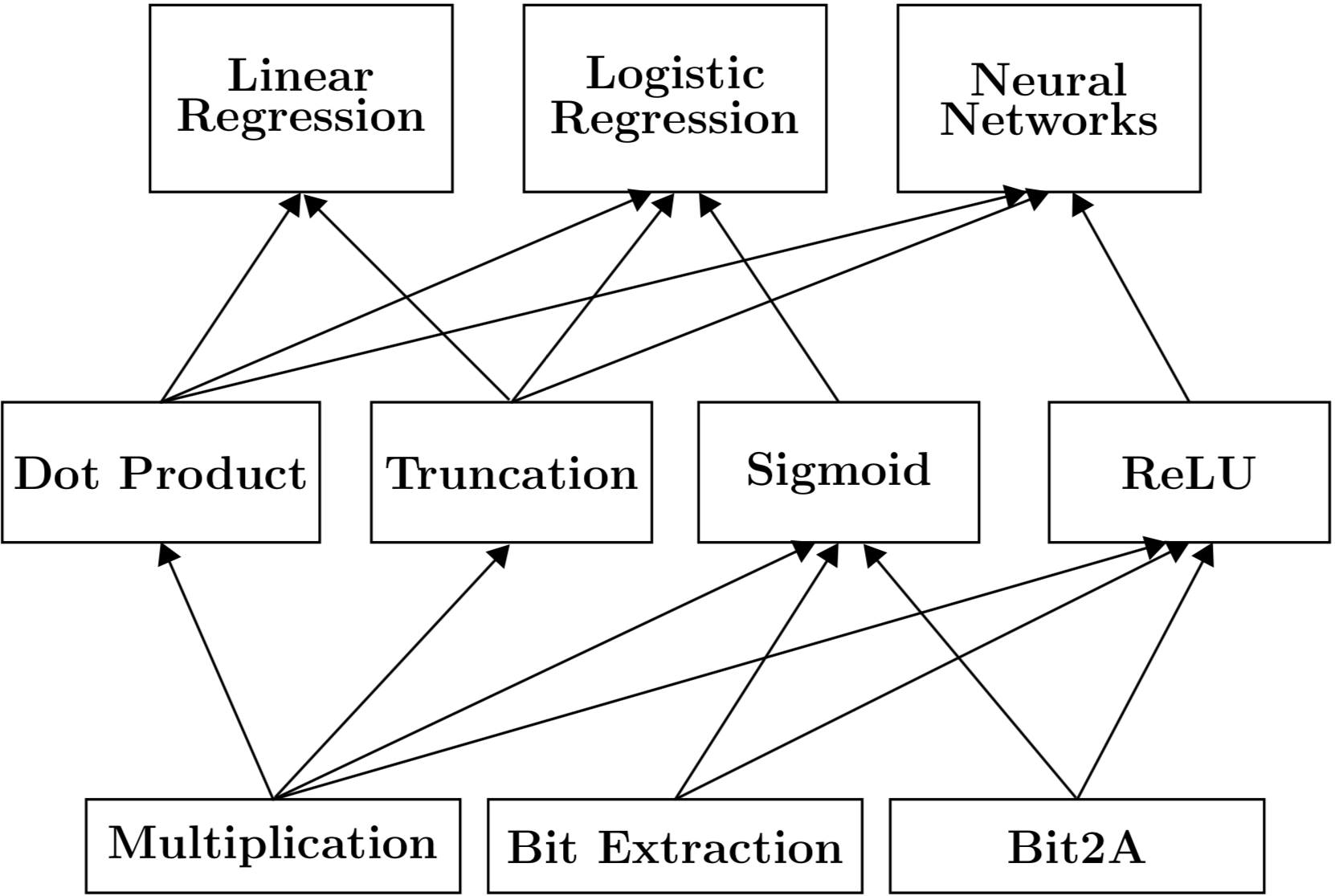
安全外包的隐私保护机器学习框架在环$\mathbb{Z}_{2^l}$上，通常，$l$取值为$64$，中间有三个服务器$P_i, i\in {0, 1, 2}$，根据安全性设置，最多一方是腐败的。当$l = 1$时，就是特殊的$\mathbb{Z}_{2^l}$，分别就是布尔共享和算术共享。文章对机器学习架构分了三层，上层是机器学习算法，比如回归和神经网络。构造成机器学习算法是算子，如下

• 点积，给定两个向量$\vec{x}, \vec{y}$，生成$\vec{x} \bigodot \vec{y}$的算术共享
• 截断，对共享值$v$，利用公开的截断参数生成算术共享的截断值
• 非线性激活函数，对于算术共享作为激活函数的变量并获取结果的算术共享

为了确保机器学习算法中参数的安全，需要下面几个操作来实现上一层算子：

• 乘法，对于任意两个共享，生成$x \cdot y$
• 位提取，给定算数共享$v$，用于生成共享的最高有效位的布尔共享
• B2A，单个共享值的布尔共享转换为算术共享

秘密共享 文章给了三种秘密共享，三种秘密共享形式，相互嵌套。对于一个秘密$v \in \mathbb{Z}_{2^l}$有：

• $[\cdot]$共享：$P_1, P_2$分别拥有$[v]_1, [v]_2, v = [v]_1 + [v]_2$
• $\langle \cdot \rangle$共享：对于三方，$P_0$持有$[\lambda_v]_1, [\lambda_v]_2$，而对于$P_i, i \in {1, 2}$持有$([\lambda_v]_i, \; v + \lambda_v)$
• $[\![ \cdot ]\!]$共享：$v$先是$\langle \cdot \rangle$共享，$P_0$持有$([\alpha_v]_1, [\alpha_v]_2)$，$P_i, i \in {1, 2}$持有$([\alpha_v]_i, \; \beta_v)$，其中$\alpha_v, \beta_v \in \mathbb{Z}_{2^l}, \beta_v = v + \alpha_v$，而$\alpha_v = [\alpha_v]_1 + [\alpha_v]_2 $

秘密共享协议目的是让$P_i$生成$v, v \in \mathbb{Z}_{2^l}$的$[\![ \cdot ]\!]$共享。预处理阶段，三方抽样随机共享分块$ [\alpha_v]_1, [\alpha_v]_2 $，能够得到共享值$ \alpha_v $，$P_1, P_2$ 抽样$\gamma_v \in \mathbb{Z}_{2^l}$，在线阶段$P_1, P_2$把$ \beta_v + \gamma_v $给$P_0$。$P_0$计算$ \beta_v$并发送给 $P_1, P_2$，$P_1$发送$ \beta_v + \gamma_v $给$P_0$，$P_2$也发送相同的哈希值给$P_0$，若收到的值不匹配，$P_0$中止协议。在ML训练中，数据拥有者输入共享，但是由数据拥有者和服务器共同执行ML阶段。一方$P$输入共享$v$，服务器$P_j, j \in {1,2}$向$P$发送$[\alpha_v]_j$，并由$P_0$发送相同的哈希值给$P$进行验证。若$P$接收到值满足一致性，则计算$ \alpha_v = [\alpha_v]_1 + [\alpha_v]_2$，否则中止协议。接着$P$计算$ \beta_v = v + \alpha_v $发送给$P_1, P_2$，$P_1, P_2$相互交换$ \beta_v$的哈希值并验证其一致性。

两服务器联合共享协议是使得$P_i, P_j$联合生成$v$的$[\![ \cdot ]\!]$共享，并且两方都知道$v$的值。$P_i$执行秘密共享协议生成$v$的$[\![ \cdot ]\!]$共享，$P_j$帮助验证其正确性。

• $(P_1, P_0)$：$P_1$执行$\Pi_{\mathsf{sh}}(P_1, \mathsf{v})$，$P_0$计算$\beta_{\mathsf{v}} = \mathsf{v} + [\alpha_{\mathsf{v}}]_1 + [\alpha_{\mathsf{v}}]_2$，$P_0$发送$\mathsf{H}(\beta_{\mathsf{v}})$给$P_2$，若接收值与$P_1$不一致，$P_2$中止协议。
• $(P_2, P_0)$：和上面一样
• $(P_1, P_2)$：预处理阶段，$P_1, P_2$共同设置随机数 $\gamma_{\mathsf{v}} \in \mathbb{Z}_{2^l}$。服务器设置 $[\alpha_{\mathsf{v}}]_1 = [\alpha_{\mathsf{v}}]_2 = 0, \; \beta_{\mathsf{v}} = \mathsf{v}$。$P_1$ 计算 $\mathsf{v} + \gamma_{\mathsf{v}}$ 给$P_0$，$P_2$设置相同的哈希值给$P_0$，若接收值与$P_1$不一致，$P_2$中止协议。

预处理阶段，$\mathsf{v}$对$P_i, P_j$都可用，在协议$ \Pi_{\mathsf{jsh}}$的执行不需要通信交互。各方服务器设置随机数$ \mathsf{r} \in \mathbb{Z}^{2^l}$，在本地设置如下图的共享。协议$ \Pi_{\mathsf{jsh}}$允许一个服务器是腐败的。

重构秘密协议$\Pi_{\mathsf{rec}}( \mathcal{P}, [\![ v ]\!])$各方从 $[\![ \cdot ]\!]$ 共享重构$ \mathsf{v} $。每一方都从另外两台服务器中的一方接受到需要的秘密共享，然后从另一方得到哈希值。通过这个哈希值确定是否重构共享。各方重构$\mathsf{v}$，服务器$P_i, i \in {0, 1, 2}$分别发送$([\![ \alpha_{\mathsf{v}} ]\!]^{\text{A}}, \mathsf{H}([\![ \alpha_{\mathsf{v}} ]\!]^{\text{B}}))$，$(\beta_{\mathsf{v}}, \mathsf{H}([\![ \alpha_{\mathsf{v}} ]\!]^{\text{A}}))$，$([\![ \alpha_{\mathsf{v}} ]\!]^{\text{B}}, \mathsf{H}(\beta_{\mathsf{v}}))$给重构方。

• $P_1$ 分别从$P_2$接收到$[\alpha_{\mathsf{v}}]_2$，从$P_0$接收到$ \mathsf{H}([\alpha_{\mathsf{v}}]_2) $
• $P_2$分别从$P_0$中接受到$[\alpha_{\mathsf{v}}]_1$，从$P_1$接收到$\mathsf{H}([\alpha_{\mathsf{v}}]_1)$
• $P_0$从$P_1$接收到$ \beta_{\mathsf{v}}$，从$P_2$接收到$ \mathsf{H}(\beta_{\mathsf{v}})$
• 若接受的值不具一致性$P_i, i \in {0, 1, 2 }$中止协议，否则计算$\mathsf{v} = \beta_{\mathsf{v}} - [\alpha_{\mathsf{v}}]_1 - [\alpha_{\mathsf{v}}]_2$

乘法协议

乘法协议$\Pi_{\mathsf{mult}}(\mathcal{P}, [\![ \mathsf{x} ]\!], [\![ \mathsf{y} ]\!])$令服务器$\mathcal{P}$有$\mathsf{x}$和$\mathsf{y}$的共享，计算$[\![ \cdot ]\!]$共享的乘法$\mathsf{z} = \mathsf{xy}$。预处理阶段，服务器$P_1, P_2$选择随机数$\gamma_{\mathsf{z}} \in \mathbb{Z}_{2^l}$，执行秘密共享协议分别得到$[\alpha_\mathsf{z}]_1, [\alpha_\mathsf{z}]_2 \in \mathbb{Z}_{2^l}$，$P_0$在本地计算$\Gamma_{\mathsf{xy}} = \alpha_{\mathsf{x}}\alpha_{\mathsf{y}}$ 。在$P_1, P_2$计算 $\begin{align*} \beta_{\mathsf{z}} &= \mathsf{z} + \alpha_{\mathsf{z}} = \mathsf{xy} + \alpha_{\mathsf{z}} = (\beta_{\mathsf{x}} - \alpha_{\mathsf{x}})(\beta_{\mathsf{y}} - \alpha_{\mathsf{y}}) + \alpha_{\mathsf{z}} \\ &= \beta_{\mathsf{x}}\beta_{\mathsf{y}} - \beta_{\mathsf{x}}\alpha_{\mathsf{y}} - \beta_{\mathsf{y}}\alpha_{\mathsf{x}} + \Gamma_{\mathsf{xy}} + \alpha_\mathsf{z} \end{align*}$

在线阶段，服务器$P_1, P_2$通过交换他们的共享$\beta_{\mathsf{z}}$在本地计算： $[\beta_{\mathsf{z}}]_j = (j-1)\beta_{\mathsf{x}}\beta_{\mathsf{y}} - \beta_{\mathsf{x}}[\alpha_{\mathsf{y}}]_j - \beta_{\mathsf{y}}[\alpha_{\mathsf{x}}]_j + [\Gamma_{\mathsf{xy}}]_j + [\alpha_\mathsf{z}]_j$。$P_1$向$P_0$发送$\beta_{\mathsf{z}} + \gamma_{\mathsf{z}}$。再通过$\mathsf{z} = \mathsf{xy}$或$\beta_{\mathsf{z}} - \alpha_{\mathsf{z}} = \mathsf{xy}$验证协议协议的正确性。

在恶意模型中，若$P_1$是腐败的，在线阶段评估$\beta_{\mathsf{z}}$的共享不正，会导致共享重构错误。可以通过执行半诚实协议时，用$\langle \cdot \rangle$共享预处理阶段的乘法三元组验证重构的正确性，但是需要较大的通信量。若可以在与计算中实现验证，减少在现阶段的通信开销。若腐败方$P_1$发送一个非法$\beta_{\mathsf{z}}$的$[\cdot]$共享，$P_0$利用$\beta_{\mathsf{x}}^\star = \beta_{\mathsf{x}} + \gamma_{\mathsf{x}}, \beta_{\mathsf{y}}^\star = \beta_{\mathsf{y}} + \gamma_{\mathsf{y}}$计算： $\begin{align*} \beta_{\mathsf{z}}^\star &= -\beta_{\mathsf{x}}^\star\alpha_{\mathsf{y}} - \beta_{\mathsf{y}}^\star\alpha_{\mathsf{x}} + 2\Gamma_{\mathsf{xy}} + \alpha_{\mathsf{z}} \\ &= (-\beta_{\mathsf{x}}\alpha_{\mathsf{y}} - \beta_{\mathsf{y}}\alpha_{\mathsf{x}} + \Gamma_{\mathsf{xy}} + \alpha_{\mathsf{z}}) - (\gamma_{\mathsf{x}}\alpha_{\mathsf{y}} + \gamma_{\mathsf{y}}\alpha_{\mathsf{x}} - \Gamma_{\mathsf{xy}}) \\ &= (\beta_{\mathsf{z}} - \beta_{\mathsf{x}}\beta_{\mathsf{y}}) - (\gamma_{\mathsf{x}}\alpha_{\mathsf{y}} + \gamma_{\mathsf{y}}\alpha_{\mathsf{x}} - \Gamma_{\mathsf{xy}} + \psi) + \psi \\ &= (\beta_{\mathsf{z}} - \beta_{\mathsf{x}}\beta_{\mathsf{y}} + \psi) - \chi \; [\chi = \gamma_{\mathsf{x}}\alpha_{\mathsf{y}} + \gamma_{\mathsf{y}}\alpha_{\mathsf{x}} - \Gamma_{\mathsf{xy}} + \psi] \end{align*}$

假设$\psi \in \mathbb{Z}_{2^l}$是$P_1,P_2$选择的一个随机数，$P_1$ 知道$\psi$，并计算$\beta_{\mathsf{z}}^\star + \psi$发送给$P_1,P_2$，然后$P_1,P_2$用知识$\gamma_{\mathsf{x}}, \gamma_{\mathsf{y}}, \psi$计算$\gamma_{\mathsf{z}} - \gamma_{\mathsf{x}}\gamma_{\mathsf{y}} + \psi$ 与$P_0$收到的$\beta_{\mathsf{z}}^\star + \chi$ 验证$\beta_{\mathsf{z}}$的正确性。这需要$P_0$计算$\chi$，$P_j, \; j \in {1,2 }$在本地计算共享$[\chi]_j = \gamma_{\mathsf{x}}[\alpha_{\mathsf{y}}]_j + \gamma_{\mathsf{y}}[\alpha_{\mathsf{x}}]_j - [ \Gamma_{\mathsf{xy}} ]_j + [\psi]_j$，$[\psi]_j$是$P_1,P_2$本地产生的随机数，不需要通信。因此$P_1,P_2$利用乘法三元组验证$\chi$的正确性。 令$\mathsf{d} = \gamma_{\mathsf{x}} - \alpha_{\mathsf{x}}, \mathsf{e} = \gamma_{\mathsf{y}} - \alpha_{\mathsf{y}}, \mathsf{f} = (\gamma_{\mathsf{x}}\gamma_{\mathsf{y}} + \psi) - \chi$，验证$\mathsf{d}\mathsf{e} = \mathsf{f}$判断$\chi$正确性。若$P_0$产生不正确的$[ \Gamma_{\mathsf{xy}} ]$共享$\Gamma_{\mathsf{xy}} + \Delta$会使得$\mathsf{de} = \mathsf{f} + \Delta \ne \mathsf{f}$。

$P_0$持有$([ \lambda_{\mathsf{f}} ]_1, [ \lambda_{\mathsf{f}} ]_2)$，$P_j, j \in \{1,2\}$持有$([ \lambda_{\mathsf{f}} ]_j, \mathsf{f} + \lambda_{\mathsf{f}})$，服务器映射$[\chi]$和$\gamma_{\mathsf{x}}\gamma_{\mathsf{y}} + \psi$到$[\gamma_{\mathsf{f}}]$和$ \mathsf{f} + \gamma_{\mathsf{f}} $。 $P_j, j \in {1,2}$ 利用随机数 $\mathsf{r} \in \mathbb{Z}_{2^l}$生成$[\psi] $，设置$[ \psi ]_1 = \mathsf{r}$和$[ \psi ]_2 = \psi - \mathsf{r}$ 。 $P_j, j \in \{1,2\}$持有$[ \Gamma_{\mathsf{xy}} ] = [ \alpha_{\mathsf{x}}\alpha_{\mathsf{y}} ]$，重构： $\begin{align*} \Gamma_{\mathsf{xy}} &= \gamma_{\mathsf{x}}\alpha_{\mathsf{y}} + \gamma_{\mathsf{y}}\alpha_{\mathsf{x}} + \psi - \chi \\ &= (\mathsf{d} + \lambda_{\mathsf{d}})\lambda_{\mathsf{e}} + (\mathsf{e} + \lambda_{\mathsf{e}})\lambda_{\mathsf{d}} + (\mathsf{f} + \gamma_{\mathsf{f}} - \gamma_{\mathsf{x}}\gamma_{\mathsf{y}}) - \gamma_{\mathsf{f}} \\ & = (\mathsf{d} + \lambda_{\mathsf{d}})(\mathsf{e} + \lambda_{\mathsf{e}}) - \mathsf{de} + \lambda_{\mathsf{d}}\lambda_{\mathsf{e}} + (\mathsf{f} - \gamma_{\mathsf{x}}\gamma_{\mathsf{y}}) \\ &= \mathsf{f} - \gamma_{\mathsf{x}}\gamma_{\mathsf{y}} + \lambda_{\mathsf{d}}\lambda_{\mathsf{e}} + (\gamma_{\mathsf{x}}\gamma_{\mathsf{y}} - \mathsf{f}) \\ &= \lambda_{\mathsf{d}}\lambda_{\mathsf{e}} = \alpha_{\mathsf{x}}\alpha_{\mathsf{y}} \\ \end{align*}$