Some Basic Protocol on BLAZE

关于安全三方计算中的一些基本协议

共享密钥设置

令F:0,1κ×0,1κ→X是一个安全伪随机函数PRF，其值域X∈Z2l

• 每个配对之间有一共享密钥，k01,k02,k12相对应于(P0,P1),(P0,P2),(P1,P2)
• 三方之间共享一个密钥kP

若服务器P0,P1非交互的采样随机值r∈Z2l，他们则调用函数 Fk01(id01)，id01是服务器每次调用PRF函数后在本地更新的计数器。这里省略选取随机数的密钥。

抗碰撞哈希函数

一个哈希函数簇H=K×L→Y，若对于所有概率多项式时间敌手A，给定Hk，其中k∈RK，都存在一个可忽略的函数negl()使得Pr[(x1,x2)←A(k):(x1≠x2)∧Hk(x1)=Hk(x2)]≤negl(κ)，这里x1,x2∈R{0,1}m,m=poly(κ)。

承若方案

令Com(x)是x的一个承诺方案，它包括两部分：隐藏和盲化。隐藏的功能让承若保证x值的隐私性，盲化则让敌手打开承若时不能区分x′≠x。一般可以通哈希函数H()构造承若，其安全性依赖于随机语言机(ROM)的证明，比如(c,o)=((h‖r),x‖r)=Com(x;r)。

乘法协议

⟨⋅⟩共享的乘法协议，对于v的⟨⋅⟩定义如下：⟨v⟩0=([λv]1,[λv]2),⟨v⟩1=([λv]1,v+λv),⟨v⟩2=([λv]2,v+λv)。同时给定d和e的⟨⋅⟩共享计算f=de的⟨⋅⟩共享。

要验证这种方法，要使证明者P在零知识的情况下V1,V2证明他知道w，并且(x,w)∈R。令ckt是被验证者的电路，使得ckt(x,w)=0 当且仅当(x,w)∈R。两个验证者共享语句x，x1,x2分别对应V1,V2，显然有x=x1‖x2。另外若|x1|=n1,|x2|=n2，则n=n1+n2，ckt上的乘法门数有M。

证明者P0选择三个多项式f(),g(),h()，分别是乘法门的左、右和输出电路。f(),g()的常数项分别为环Z2l上的随机元素z1,z2，h()的常数项则为z1z2，更详细的如下。P0对多项式f(),g(),h()进行插值计算，f(),g()最多M次多项式，h()多项式最多是2M次。令π是一个证明(w,z1,z2,ch)∈Z2ℓ，其中ch是多项式h()的系数。证明的大小是σ=s+d+3，s是目击者的大小。P0向π提供加法共享πi给验证者，πi是Pi,i∈{1,2}。若P0是诚实方，则∀r∈Z2ℓ,h(r)=f(r)g(r)和h(M)=0。

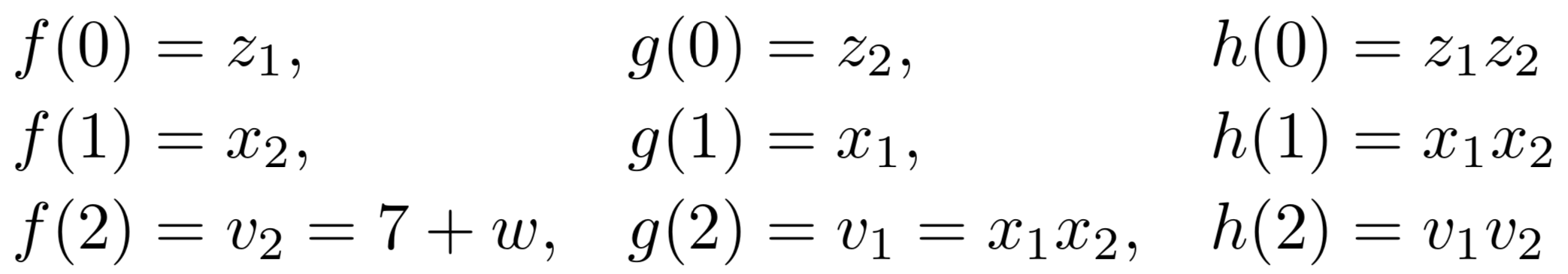
验证者P1,P2一起随机生成r∈Z2ℓ∖{z1,z2}并生成相对应的查询向量qf,qg,gf∈Zn+σ2ℓ。验证者P1,P2从qf,qg,qh中构造三个查询向量。更进一步，相对应于多项式f()，验证者P1,P2从qf中构建向量Qif∈Fni+σ,i∈{1,2}，这样，前ni个位置被保留给对应于后面是qf的xi项。 然后，验证者P1,P2本地计算向量(xi‖πi)和Qif点积fi(r)=(xi‖πi)⊙Qif并发送给P1。一旦P1接收到fi(r)的共享就计算f(r)=f1(r)+f2(r)。这是由于每个查询向量定义了输入x和证明π的线形组合。因此，验证者用输入xi和加法共享πi的部分，形成查询答案的加法共享，这个答案在随机数r处评估的多项式。 相似的步骤，可以让P1获得多项式g(r),h(r)，若h(r)≠f(r)g(r)，则P1中止协议。若一个想作弊的验证者要通过验证的概率最大为2M−12ℓ−2，ℓ足够大的话，概率可以忽略不计。 对于第二个验证，即h(M)=0，验证者用相同的方式生成查询向量q。对于i∈{1,2},Pi的查询Qi计算hi(M)并发送h(M)的共享给P1。若h(M)≠h1(M)+h2(M)=0，则P1​中止协议。这种查询采用了2轮的完全显性交互喻示器证明，查询复杂度为O(√n)，其中n是输入的大小。

安全性

文章用标准现实/理想模型证明协议构造的安全性。令A是现实世界的敌手，表示各方服务器中P中的腐败方。用S表示A的理想世界的敌手(也就是模拟器)，它是一个诚实方的服务器，模拟敌手A在执行协议中收到的信息。仿真器初始化布尔变量flag=0，它表示诚实方服务器在协议执行期间是否出现中止操作。若协议中止，则flag=1。对于电路ckt，仿真器从共享输入阶段开始，S将诚实方输入设置为0。从共享协议Πsh，S提取A的输入，这使得S或得电路ckt的全部输入，这反过来有能让S​知道所有中间值和电路的输出。通过分别模拟参与方P0,P1的攻击行为，证明协议的安全性。

共享协议Πsh的理想功能实现 P0为腐败方时仿真器执行协议 P1为腐败方时仿真器执行协议